要旨
詳細な地下構造は、震源決定精度の向上はもとより、地震が発生する場所の物質や温度などを推定するのに役立ち地震発生のメカニズムを解明する上で重要である。詳細な地下構造を求めるためにトモグラフィ※1は広く利用されておりトモグラフィでは地震波の波形計算は必要不可欠なものである。不均質な構造での波線計算はPseudo-Bending法(Um and Turber,1987)に代表されるような非常に効率的な手法が開発され広く使用され、相当詳細な地下構造が解明されている。一方、不均質でかつ異方性※2をもった構造での波線計算は一般的に複雑(例えばČervený, 2001)になり、従来の不均質ではあるが等方的な媒質での計算で代用している研究が多く、簡単で効率的な手法が求められている。最短経路法※3を等方的な媒質に適用する初期の例はNakanishi and Yamaguchi(1986)にみられる。最短経路法では対象領域に仮想的に分布させた点(ノード)を結ぶ経路を波が伝わる時間が分かれば計算できるので、異方性媒質への適用も容易である。しかし、計算時間がかかるのが短所であった。本研究では、波線の周辺に計算すべきノードを絞る(図)という工夫をすることにより計算時間が劇的に短縮できることを示した。これによって異方性構造のトモグラフィでも異方性を考慮した波線計算を実施することが容易になり、異方性構造の解明がさらに進むことが期待できる。異方性は鉱物の種類、層状構造、力の方向などに関係しているので、それらについての新たな知見を得ることができるようになり、地震の発生する場所の物性の理解がさらに進展するであろう。なお、本研究では改善効果を示すためには等方性媒質での計算で十分なので異方性媒質での計算は行っていない。
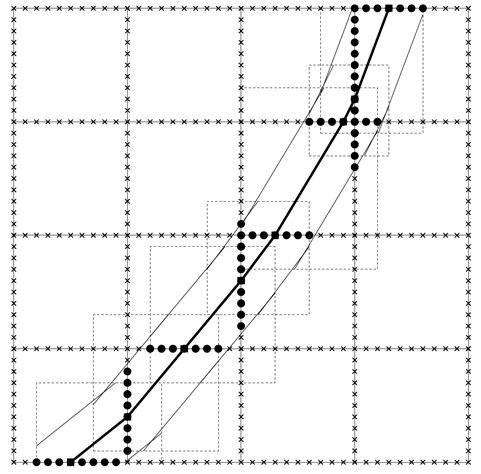 図
図.通常の最短経路法では、まず、対象領域を矩形のセルに分割し、セル境界上にノードを配置、セルごとにセル表面の全ノードを結ぶ全経路を想定する。本研究では基準波線(太線)に沿った一定距離(基準波線両側の細線)以内のノードのみ(黒丸印)を取り出し、そのノード間の経路のみに計算対象を減らすことにより、計算時間の短縮に成功した。実際の計算手順としては、セル数、ノード数が少ない設定から計算を初めて、そこで得られた波線を次のセル数、ノード数を増やしたときの基準波線として使用する。計算された波の到達時間が収束するまでセル数、ノード数を増やしながら繰り返す。(なお、図中の基準波線沿いに点線で描いたいくつかの矩形は、基準波線からの距離を計算するノードの範囲をあらかじめ大雑把に絞るために設定したものだが細かすぎるので説明略。)
用語の説明
※1 トモグラフィ
地震学の世界では、震源から観測点に伝わってくる地震波の到達時間の速い遅いのデータを大量に用いて計算機の能力を活用し地下構造を推定する手法を指す。医療診断分野のCTをヒントに開発されたともいわれている。地震学で用いられるいろいろなトモグラフィ手法については例えばIyer and Hirahara (1993)を参照のこと。
※2 異方性
波の進む方向によって速さが異なるといった方向によって異なる性質をもっていること。鉱物の結晶、硬いものと柔らかいものが層状に重なっているもの(マグマの岩脈が貫入しているところ、など)。身近なものでは紙が厚く重なった辞書や電話帳もそうである。働いている力の方向によって結晶の方向や岩脈の方向が揃う傾向があるので、力の作用する方向の推定にも利用できる。一方、方向に影響されない場合は「等方的」と呼ぶ。
※3 最短経路法
始点から終点まで、どの経路をたどれば最短時間で到着できるか、という問題を解く方法。グラフ理論で対象とする問題の一つ。グラフ理論そのものについては例えばCormen et al. (2009)を参照のこと。
学術雑誌名など発表した媒体の情報
雑誌情報: Geophysical Journal International, 225, 729-743 (2021)
タイトル: Efficient seismic ray tracing based on the shortest path method
著者: Shoji Sekiguchi
DOI番号:
https://doi.org/10.1093/gji/ggab001
参考文献
Červený, V., 2001, Seismic Ray Theory, Cambridge University Press, Cambridge.
Cormen, T.H., C.E. Leiserson, R.L Rivest, and C. Stein, 2009, Introduction to Algorithms, Third Edition, The MIT Press, Massachusetts.
Iyer, H.M. and K. Hirahara, 1993, Seismic Tomography: Theory and Practice, Chapman & Hall, London.
Nakanishi, I. and K. Yamaguchi, 1986, A numerical experiment on nonlinear image construction from first-arrival times for two-dimensional island arc structure, J. Phys. Earth, 34, 195-201.
Um, J. and C. Thurber, 1987, A first algorithm for two-point seismic ray tracing, Bull. seism. Soc. Am.,77, 972-986.
